Un mucchio di sassi rotanti disseminati nello spazio tra Marte e Giove, laddove sarebbe stato meglio che ci fosse un bel pianeta. Punti luminosi con la pessima abitudine di rovinare le fotografie a lunga posa con le loro tracce, senza peraltro fornire alcuna utile informazione, a parte l’evidente e fastidioso segno del loro percorso in cielo. Questo sono stati considerati per lungo tempo gli asteroidi, corpi celesti troppo poco interessanti per giustificare importanti programmi di ricerca loro dedicati.

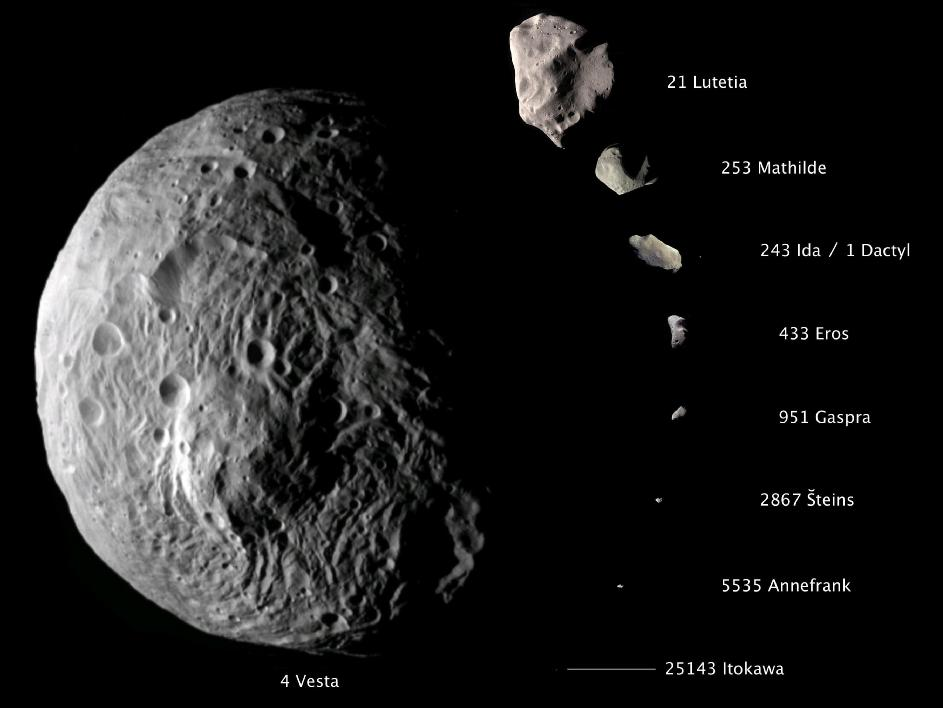
Comparative imagery of nine asteroids. With a diameter of about 330 miles (530 kilometers), Vesta dwarfs all of these small bodies. Many scientists think it’s a protoplanet left over from the solar system’s first few million years.
Credit: NASA/JPL-Caltech/JAXA/ESA
Negli ultimi decenni ci si è resi conto che si trattava, invece, di tasselli fondamentali per capire l’origine del nostro Sistema Solare e, in ultima istanza, di noi stessi. Perché una rivoluzione così radicale potesse avvenire, erano però necessarie idee molto forti, di quelle che in qualche modo segnano un prima e un dopo. Nel caso in questione si è trattato di due distinte prese di coscienza, legate rispettivamente alla vita e alla morte, una sorta di Eros e Thanatos su scala planetaria.
Da sempre l’uomo si chiede quale sia stata l’origine dell’Universo. Alcuni secoli di ricerche scientifiche non hanno ancora fornito risposte definitive, ammesso che ciò sia possibile. Tuttavia, hanno permesso di definire con sufficiente grado di precisione le caratteristiche principali del grande affresco cosmico. Restano però bisognose di ulteriori ed approfondite indagini alcune questioni cruciali, una delle quali ci interessa direttamente. Come si è formato il Sistema Solare ed in particolare il bel pianeta blu che ci ospita? Si potrebbe pensare che per venirne a capo, basti studiare in maniera accurata lo straordinario campionario di strutture geologiche disseminate sul globo terracqueo, la sua correlazione con le immani forze che ancora oggi agiscono all’interno del pianeta e l’interazione con gli elementi atmosferici e marini che ne hanno modellato il paesaggio per miliardi di anni. Tutto ciò è molto sensato, ed in effetti è quanto tentano di fare, con ottimi risultati, schiere di geologi, oceanografi e meteorologi. Ma la descrizione, per quanto dettagliata, deve inevitabilmente arrestarsi davanti ad una sorta di piccolo orizzonte degli eventi terrestre, costituito dal momento in cui l’intero pianeta era poco più di una massa fusa in continua trasformazione. All’interno dell’immensa sfera infuocata, sconvolgimenti di straordinaria potenza rimescolavano da cima a fondo tutta la materia, facendo così perdere quasi completamente le informazioni riguardanti il materiale primigenio da cui tutto aveva preso forma. Fine della storia e delle nostre ricerche? Fortunatamente no.
Un raffinato lampadario di vetro di Murano ci dice poco della sua origine, ma se guardandoci attorno troviamo pezzi di vetro semifuso, una fornace ancora accesa, un mucchietto di silice ed un pizzico di soda in un sacchetto, forse possiamo ancora ricostruire la sequenza delle trasformazioni che l’hanno portato ad essere quel che è. Su scala planetaria, il mucchietto di sabbia con i resti di fusione è rappresentato dagli asteroidi e dalle comete, corpi le cui caratteristiche chimiche e isotopiche sono state poco o punto modificate da processi di differenziazione e di evoluzione termica su larga scala e che conservano ancora oggi al loro interno preziosissime informazioni relative alla composizione della nebulosa primordiale. Avanzi, certo, di uno dei più straordinari processi di costruzione di nuovi mondi che si possa immaginare, ma al contempo, preziosi scrigni ricolmi di gioielli e, secondo alcuni, perfino diretti portatori della vita sulla Terra, un gesto degno di un magnifico Eros cosmico.
E Thanatos? In una notte calma e senza vento dirigiamo il nostro fidato telescopio verso il primo quarto di luna. Nell’oculare balza subito all’occhio il grande bacino circolare del Mare Serenitatis interamente ricoperto di lava, nonostante i quasi 700 km di diametro.
 In direzione opposta, verso il polo sud lunare, un’incredibile selva di crateri di tutte le dimensioni ricopre completamente la regione. Aumentando gli ingrandimenti, anche quelle zone che in precedenza sembravano lisce, si rivelano essere una moltitudine di piccoli crateri addossati gli uni agli altri. I più antichi sono stati quasi del tutto demoliti dai nuovi arrivati che hanno saturato completamente ogni spazio disponibile, distruggendo gli originali terrazzamenti e riempiendo a forza le platee, quasi vigesse una sorta di horror vacui che richiama alla mente certe architetture barocche leccesi o siciliane.
In direzione opposta, verso il polo sud lunare, un’incredibile selva di crateri di tutte le dimensioni ricopre completamente la regione. Aumentando gli ingrandimenti, anche quelle zone che in precedenza sembravano lisce, si rivelano essere una moltitudine di piccoli crateri addossati gli uni agli altri. I più antichi sono stati quasi del tutto demoliti dai nuovi arrivati che hanno saturato completamente ogni spazio disponibile, distruggendo gli originali terrazzamenti e riempiendo a forza le platee, quasi vigesse una sorta di horror vacui che richiama alla mente certe architetture barocche leccesi o siciliane.

Terminatore lunare nei pressi del cratere Ticho – 2004
Oggi sappiamo che questi crateri sono stati generati da impatti di un gran numero di asteroidi e di meteoriti con la superficie del nostro satellite, soprattutto nelle prime fasi dell’evoluzione del Sistema Solare. Anzi, la Luna stessa si è con molta probabilità formata dalla collisione con la giovane Terra di un planetoide delle dimensioni di Marte. Anche il nostro pianeta ha sicuramente sperimentato questa fase di bombardamento cosmico dalle conseguenze più o meno catastrofiche che, seppur diradandosi progressivamente col passare del tempo, non è mai cessato del tutto.
Almeno in un caso, circa 65 milioni di anni fa, si ha ormai la quasi certezza che la caduta di un asteroide di qualche chilometro di diametro abbia portato ad una delle più grandi estinzioni di massa nella storia evolutiva della biosfera, la ben nota scomparsa dei dinosauri. Per la verità, secondo autorevoli studiosi, i mammiferi, compresi noialtri, devono la loro esistenza proprio all’immane catastrofe che seguì l’impatto e che spazzò via, in un colpo solo, i giganteschi rettili che avevano regnato incontrastati fino a quel momento. Tuttavia, lo stesso meccanismo che ha forse permesso la nostra esistenza potrebbe un giorno, si spera mai, portare alla nostra estinzione.
Ed ecco la seconda idea fondamentale. Gli asteroidi possono essere una grave minaccia per la sopravvivenza della nostra specie. In particolare, è diventato evidente che è di vitale importanza individuare tutti quei corpi che, per le loro caratteristiche dinamiche, possono entrare in rotta di collisione con la Terra, i cosiddetti PHAs (Potential Hazardous Asteroids, al 27 Gennaio 2015 sono 1541 quelli noti) e studiarne le caratteristiche, soprattutto la struttura interna e la loro composizione chimica e mineralogica, al fine di poter approntare le eventuali contromisure con cognizione di causa. Un impatto di un asteroide metallico avrebbe, infatti, conseguenze ben più catastrofiche di quello di un analogo roccioso, costituito da un aggregato incoerente di frammenti tenuti assieme dalla gravità.
I PHAs sono una piccolissima frazione della più numerosa famiglia dei NEO (Near Earth Object), costituita da una popolazione piuttosto eterogenea di corpi minori comprendente asteroidi, comete attive ed estinte e corpi progenitori di alcune classi di meteoriti. Provengono da tutte le regioni del Sistema Solare e sono caratterizzati dall’avere orbite caotiche e instabili che, nel volgere di pochi milioni di anni, concludono la loro esistenza cadendo sul Sole o impattando uno dei pianeti interni, se non sono finiti nel frattempo su orbite che li portano ad essere espulsi dal Sistema Solare.
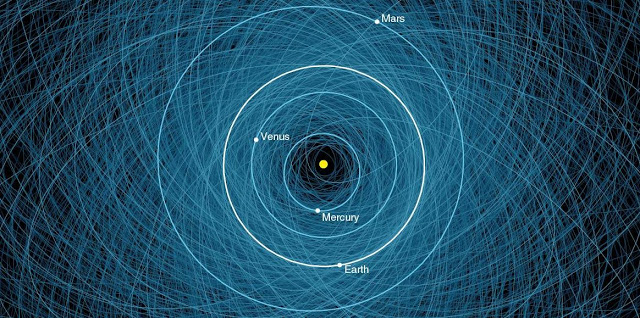
An image mapping the orbits of all the potentially hazardous asteroids (PHAs) known. Image Credit: NASA/JPL-Caltech
La loro breve esistenza, su tempi scala cosmici, implica che la popolazione di NEO che osserviamo ai giorni nostri, non può certamente essere la stessa di quella che avremmo trovato anche solo qualche centinaio di milioni di anni fa. Deve perciò esistere un qualche meccanismo che rifornisce continuamente la popolazione dei NEO, compensandone le perdite e mantenendo relativamente alta nel tempo la probabilità che uno di essi finisca col prenderci di mira. Sono state individuate varie sorgenti che possono iniettare questi oggetti verso il Sistema Solare interno, portandoli ad intersecare o quantomeno ad avvicinarsi all’orbita terrestre. La parte del leone sembra svolta dalle potenti risonanze esistenti nella Fascia Principale, in particolare quelle con Giove, e dagli incontri ravvicinati con Marte. Per valutare correttamente le probabilità di un eventuale impatto è fondamentale conoscere con grande precisione i parametri orbitali.
Se sulla base di accurate misure astrometriche sembra che il rischio di collisione non sia trascurabile, osservazioni condotte con potenti radiotelescopi possono indicare le reali possibilità. Il fascio ad alta potenza emesso da un radar, 1Megawatt nel caso del radiotelescopio di 305 metri di Arecibo, è estremamente coerente, cosicché la fase dell’onda elettromagnetica è la stessa su tutto il fronte d’onda. Sfruttando la tecnica del time-delay, ossia della misura del tempo che intercorre tra l’emissione del fascio e la ricezione dell’eco, è possibile determinare la distanza del target con una precisione attorno ai cento metri e stimare la componente della velocità lungo la linea di vista, con un margine d’errore dell’ordine del millimetro al secondo, come dire che si potrebbe ricostruire il moto di una formica che si arrampica su un muro. L’analisi dell’eco permette anche di determinare le proprietà fisiche della superficie dell’asteroide. La rugosità superficiale influenza il modo in cui l’onda radar è riflessa: una superficie liscia tende a mantenere la coerenza del fascio al contrario di una scabra, mentre una metallica riflette molto più intensamente di una rocciosa coperta da regolite. Inoltre, siccome l’oggetto è in moto, la frequenza dell’onda riflessa è diversa da quella incidente, per effetto Doppler. Un’accurata analisi di queste variazioni consente di ricostruire la forma dell’asteroide con sorprendente precisione, ottenendo una sorta di fotografia, tanto più dettagliata quanto più l’oggetto è vicino. La potenza dell’eco ricevuta è, infatti, inversamente proporzionale alla quarta potenza della distanza dell’oggetto, il che spiega come mai i NEO, transitando in certi casi a distanza inferiore a quella Terra-Luna, sono i candidati ideali per questo tipo di indagini.
Proprio ieri, 26 Gennaio 2015, gli scienziati della NASA, sfruttando l’antenna di 70m di Goldstone, hanno ricostruito le immagini radar dell’asteroide 2004 BL86 che stava transitando a circa 1.2 milioni di chilometri dalla Terra, e che ha riservato una gradita sorpresa: è un asteroide di circa 325metri con una piccola luna di 70 metri che gli orbita attorno.

This GIF shows asteroid 2004 BL86, which safely flew past Earth on Jan. 26, 2015. Image Credit: NASA/JPL-Caltech
Solo di recente si è iniziato a studiare anche gli oggetti della Fascia Principale. La prima osservazione di questo tipo è stata quella di (216) Kleopatra, un asteroide lungo circa 217 km e largo 94 km, dalla caratteristica forma ad osso. Le osservazioni sono state condotte ad Arecibo, quando l’asteroide si trovava ad oltre 170 milioni di km di distanza da Terra; il fascio radar impiegava circa 19 minuti per raggiungerlo e tornare al ricevitore.
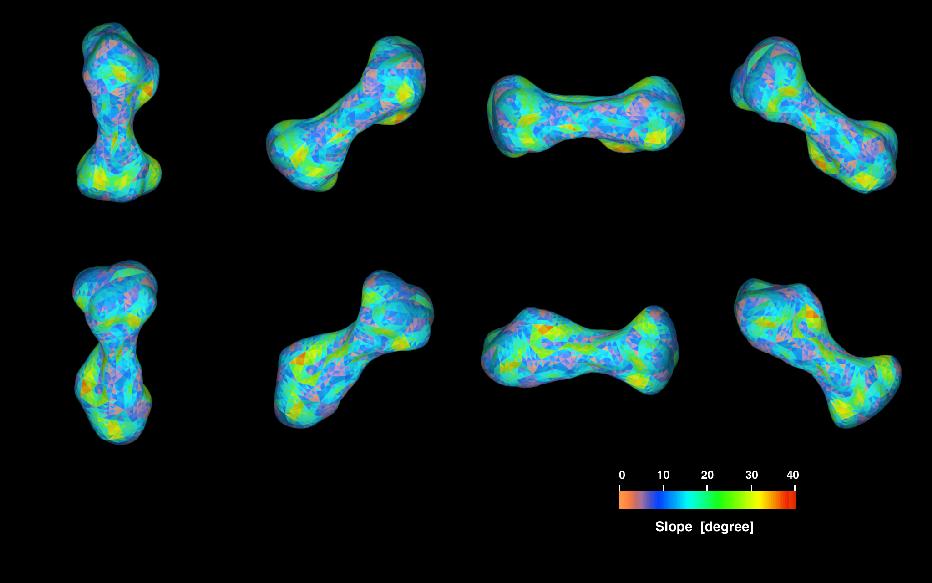
Ricostruzione radar della forma dell’asteroide (216) Kleopatra ottenuta col grande radiotelescopio di Arecibo, sfruttando la tecnica del Doppler imaging. Da notare la notevole finezza dei dettagli superficiali, soprattutto in considerazione del fatto che, al momento dell’osservazione, l’asteroide si trovava ad oltre 170 milioni di km di distanza.
Il grande limite delle misure radar sta nel fatto che è possibile studiare un numero molto limitato di oggetti, almeno con gli attuali strumenti a disposizione. Viceversa, i planetologi vorrebbero poterne osservare il più grande numero possibile, per poter poi applicare considerazioni di tipo statistico, inevitabili quando si tratta di caratterizzare una popolazione che, verosimilmente, è composta di parecchi milioni di oggetti. Nell’attesa dei dati della missione spaziale GAIA, che si ripromette di rivoluzionare per quantità e qualità le conoscenze sugli asteroidi, le osservazioni fotometriche condotte da Terra continuano ad essere, da questo punto di vista, uno strumento fondamentale, poiché permettono di ottenere un discreto numero di informazioni, tutto sommato in maniera relativamente semplice anche con strumentazione commerciale.
Gli asteroidi hanno forme più o meno allungate e più o meno stravaganti, conseguenza il più delle volte di complicate esistenze dominate da violente collisioni reciproche. Se nelle prime fasi della formazione del Sistema Solare i detriti collidevano a velocità relativamente basse, favorendo in questo modo il progressivo accrescimento e la formazione di corpi di grandi dimensioni, la successiva evoluzione delle orbite, soprattutto di quelle caratterizzate da alte eccentricità ed inclinazioni, ha fatto sì che le collisioni avvenissero a velocità comprese tra i 5 ed i 20 km/s conferendo alle collisioni un carattere distruttivo. Spesso la violenza degli impatti è stata tale da sbriciolare letteralmente i corpi coinvolti. In alcuni casi dalle collisioni sono emerse le cosiddette famiglie dinamiche, costituite da piccoli e grandi oggetti con elementi propri e proprietà fisiche simili a quelle del corpo genitore.
Accurate simulazioni numeriche hanno dimostrato, per esempio, che le famiglie di Eunomia e Koronis hanno avuto un’origine di questo tipo e che tutti gli oggetti di dimensioni maggiori sono probabilmente costituiti di aggregati di frammenti debolmente legati tra loro (rubble-pile), tenuti assieme dalla gravità e dalle forze di stato solido. Un altro sottoprodotto di questo tipo di evento è la formazione di satelliti attorno al corpo principale. Attualmente sono stati individuati satelliti di asteroidi nella Fascia Principale, tra i NEO e tra i transnettuniani. E’ di qualche anno fa la scoperta di un asteroide triplo, (87) Sylvia, un oggetto di 280km di diametro con due piccole lune, rispettivamente a 710 e 1360km di distanza, che ruotano attorno ad esso su orbite equatoriali, circolari e prograde il che suggerisce con forza un’origine comune. In genere i satelliti sono piccoli rispetto ai corpi principali, ma a volte, come nel caso di (90) Antiope, le dimensioni sono confrontabili, tanto che, più correttamente, si deve parlare di asteroidi doppi.

VLT observations of the double asteroid (90) Antiope during 2004. The adaptive optics NACO instrument was used, allowing the astronomers to perfectly distinguish the two components and so, precisely determine the orbit. The two objects are separated by 171 km, and they perform their celestial dance in 16.5 hours.
Il grande interesse per gli asteroidi binari o multipli deriva dal fatto che dallo studio dell’orbita dei componenti è possibile determinare la loro massa tramite le leggi di Keplero e, se si dispone anche di una stima delle dimensioni, di ricavare la densità, parametro fondamentale per capire la struttura interna dell’oggetto. (87) Sylvia, per esempio, è sicuramente un rubble-pile con una significativa percentuale di spazi vuoti al suo interno. L’importanza di questo dato risiede nel comportamento di questi corpi in caso di collisioni successive. La presenza di molti vuoti e giunzioni al loro interno fa sì che riescano ad assorbire in maniera molto efficiente l’energia dell’impatto, con la produzione di coltri di ejecta e notevoli quantità di regolite come nel caso di (433) Eros o, addirittura, la formazione di crateri di dimensioni confrontabili con quelle dell’asteroide stesso, senza distruggerlo. Emblematico in questo senso è (253) Mathilde, la cui superficie è dominata da grandi crateri da impatto di diametro superiore al raggio medio dell’asteroide.

From fifty kilometers above asteroid Eros, the surface inside one of its largest craters appears covered with an unusual substance: regolith. The thickness and composition of the surface dust that is regolith remains a topic of much research. Much of the regolith on (433) Eros was probably created by numerous small impacts during its long history.

An image of Asteroid (253) Mathilde taken by the space probe NEAR Shoemaker on 27 June 1997 from a distance of 2400 km. It is lit up by the sun from the top right. The part of the Asteroid visible in the picture has Dimensions of 59 km x 47 km. On the surface, numerous large craters are visible, like the Large Crater in the Center, named Karoo, which is more than 30 km wide. Most of it is shaded in the picture.
Un notevole salto di qualità nello studio fotometrico degli asteroidi si è avuto, come per tutti i settori dell’Astrofisica, con l’introduzione dei sensori a stato solido, i cosiddetti dispositivi ad accoppiamento di carica o CCD. Attualmente con un telescopio di 20 cm di diametro è possibile studiare asteroidi di 14-esima magnitudine con un buon grado di precisione ed affidabilità laddove, prima dell’avvento dei CCD, sarebbe stato necessario uno strumento di apertura nettamente maggiore.
Tutte le curve di luce a colori riportate di seguito sono state ottenute ormai una decina di anni fa presso l’Osservatorio Astrofisico R.P.Feynman con un Dall-Kirkham di 21cm di apertura nell’ambito dell’ALP (Asteroid Lightcurve Program) che avevo attivato in quegli anni.
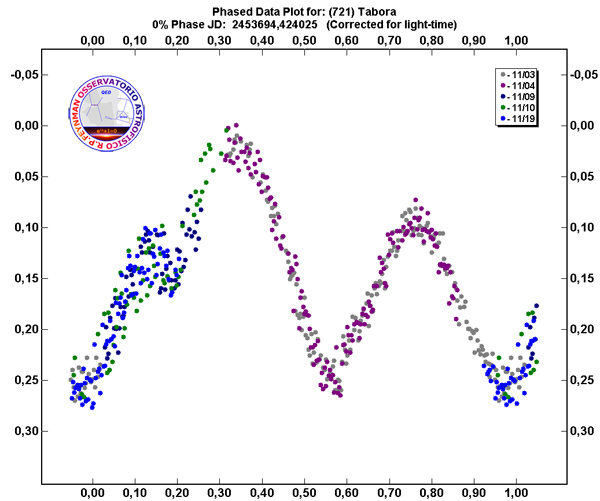
In un ideale passaggio di consegne generazionale e tecnologico ecco la curva di luce di (721) Tabora il cui periodo di rotazione stimato da Zappalà et al. nel 1989 era di 8 ore (Rotational properties of outer belt asteroids, Based on observations performed mainly at the European Southern Observatory, ESO, La Silla, Chile. Icarus 82, 354-368.) e che riuscii a rifinire in 7.982 ± 0.001 ore
Dall’analisi della curva di luce si ricava innanzitutto il periodo di rotazione dell’asteroide che, in genere, ruota attorno ad un asse fisso, mostrando all’osservatore le superfici di area massima e minima in maniera ciclica.

Images of (433) Eros from NEAR Shoemaker.
Courtesy of JHU/APL. Two days after NEAR Shoemaker began its orbit of Eros, the spacecraft captured this rotation movie as it moved closer to the asteroid. The movie shows a full rotation on February 16, 2000, as viewed from a range of about 340 kilometers
Un sufficiente numero di curve di luce, ottenute con osservazioni a diverse longitudini eclittiche e distribuite nell’arco di tre o quattro apparizioni, consente di determinare la direzione dell’asse di rotazione. Inoltre, permette la costruzione di un modello tridimensionale abbastanza dettagliato della struttura su larga scala dell’asteroide mediante la tecnica matematica dell’inversione delle curve di luce.
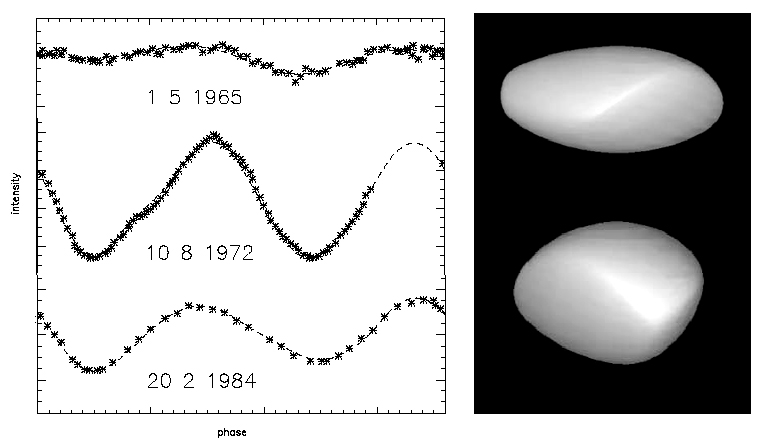
Tre curve di luce dell’asteroide (43) Ariadne affiancate dal modello tridimensionale ottenuto con la tecnica matematica dell’inversione di un cospicuo numero di curve di luce, acquisite in epoche differenti. La diversa forma e ampiezza delle curve è dovuta al cambiamento delle condizioni di illuminazione durante ogni apparizione. (Kaasalainen et al. Icarus 159 (2002) mod.)
Il motivo per cui è necessario osservare l’oggetto sotto diverse prospettive è che in questo modo l’illuminazione laterale e radente mette in evidenza, grazie al gioco di luci e di ombre, anche le eventuali irregolarità nella forma, almeno su scala macroscopica. Un asteroide sferico non mostra alcuna variazione significativa nella curva di luce nel corso della sua rotazione, ma anche un oggetto fortemente elongato esibisce un comportamento analogo se osservato in direzione del suo polo. Ma, mentre nel primo caso non ci sono variazioni di sorta nemmeno se la visione è equatoriale, nel secondo si ha un’alternanza evidentissima di massimi e minimi, dovuta alla grande differenza nell’estensione dell’oggetto lungo gli assi perpendicolari a quello di rotazione. Non è raro, in questo caso, riscontrare ampiezze nella curva di luce anche di una magnitudine che, nel caso di asteroide approssimabile nella forma ad un ellissoide di Jacobi, implica un rapporto di circa 5/2 tra i due assi principali.
In linea di principio per ottenere una buona curva di luce è sufficiente un centinaio di punti ben distribuiti lungo il periodo. Tuttavia, un numero maggiore è sicuramente preferibile, sia per evidenziare eventuali irregolarità morfologiche, sia per minimizzare gli errori nelle misure dovuti, per esempio, a peggioramento delle condizioni meteo durante le osservazioni. La maggior parte degli asteroidi ruota con periodi compresi tra 6 e 12 ore perciò un paio di notti di misure, almeno durante l’inverno, sono sufficienti per determinare in maniera accurata il periodo. E’ opportuno però aggiungere una terza sessione a distanza di qualche giorno per ottenere una maggiore precisione.
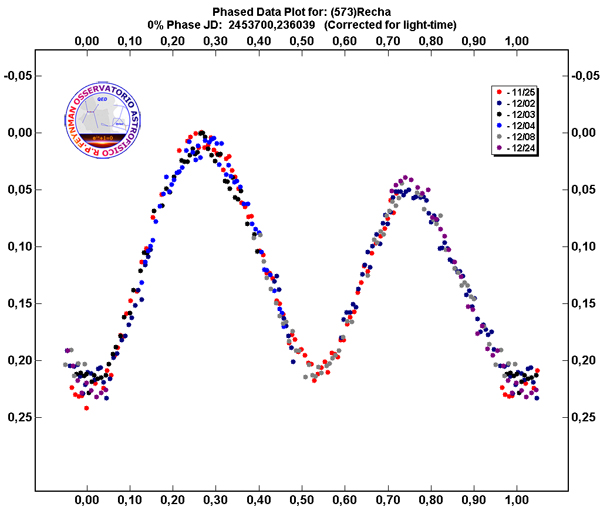
Generalmente la curva di luce ha un andamento di tipo sinusoidale con due massimi e due minimi, spesso di altezza e profondità differenti. Un esempio è la curva di luce di (1459) Magnya; quest’oggetto era stato scelto come obiettivo della prima osservazione interferometrica di un asteroide con il VLTI dell’ESO, con l’intento di ricavarne il diametro per via diretta. La curva di luce, oltre a permettere di rifinire il periodo di rotazione, è stata utile anche per individuare in quale fase si trovava l’asteroide al momento delle osservazioni interferometriche.
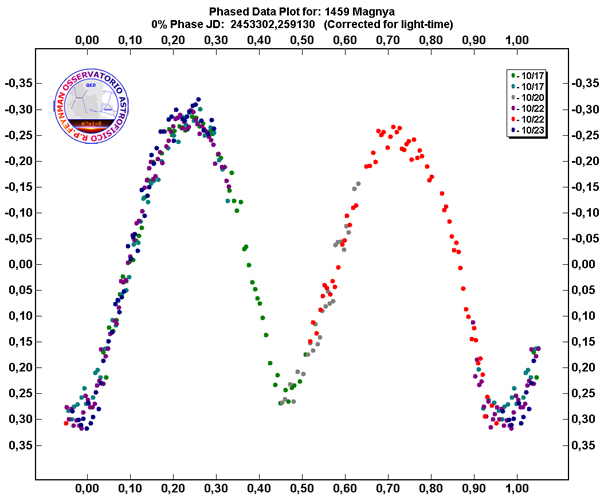
Curva di luce di (1459) Magnya, raro asteroide della zona esterna della Fascia principale con una crosta basaltica e target della prima osservazione interferometrica col VLTI dell’ESO (Delbò et al. “MIDI observations of (1459) Magnya: First attempt of interferometric observations of asteroids with the VLTI”, Icarus, vol. 181, pp. 618-622 (2006)
Analoghe considerazioni valgono quando lo studio fotometrico è contemporaneo alle osservazioni radar, soprattutto se di oggetti non ancora ben caratterizzati. Alcuni asteroidi di dimensioni abbastanza contenute e monolitici hanno periodi di rotazione di poche ore o addirittura di pochi minuti. Se fossero di tipo rubble-pile, sarebbero rapidamente disgregati dalla forza centrifuga. La barriera tra i due tipi sembra collocarsi attorno alle 2.25 ore, ma ulteriori osservazioni possono migliorare in modo rilevante la statistica relativa. Esistono anche asteroidi con periodi di rotazione di giorni e perfino di mesi ed altri per i quali questo dato non è univocamente determinabile, come i cosiddetti asteroidi ubriachi. Si tratta di oggetti che non ruotano attorno a nessuno degli assi principali d’inerzia, ed anzi la direzione dell’asse di rotazione è continuamente variabile nel tempo. Celebre è il caso di (4179) Toutatis, un asteroide costituito da due corpi irregolari di 2.5 e 4 chilometri, praticamente a contatto, la cui rotazione è il risultato di due diversi tipi di moto, con periodi di 5.4 e 7.3 giorni terrestri, che si combinano in maniera tale che l’orientazione nello spazio di questo asteroide, non si ripete mai con le stesse modalità. Si tratta di una sorta di relitto che testimonia la grande complessità della dinamica collisionale nelle prime fasi della formazione del Sistema Solare. A causa degli attriti e delle tensioni interne, che dissipano grandi quantità di energia, queste rotazioni ubriache tendono a regolarizzarsi su tempi scala dell’ordine di qualche decina di milioni di anni, in maniera tanto più rapida quanto più la rotazione è veloce per una data dimensione dell’asteroide, ma Toutatis ruota così lentamente che il tempo necessario perché questo processo di stabilizzazione diventi effettivo è più lungo di quello trascorso dalla formazione del Sistema Solare.
Anche quando la rotazione non è “ubriaca”, la determinazione del periodo, a volte, è un vero rompicapo e sono necessarie diverse notti di misure per risolvere il problema. Può succedere, infatti, che l’asteroide sia binario, cosicché nella curva di luce si sovrappongono periodi differenti e perfino eclissi. Un campanello d’allarme può essere la presenza di un numero maggiore dei canonici due estremi per ciclo. Un asteroide nella lista dei sospetti binari, che esibisce ben quattro massimi e minimi, è (2346) Lilio. Potrebbe anche trattarsi di un oggetto singolo di tipo ellissoidale, ma molto deformato.
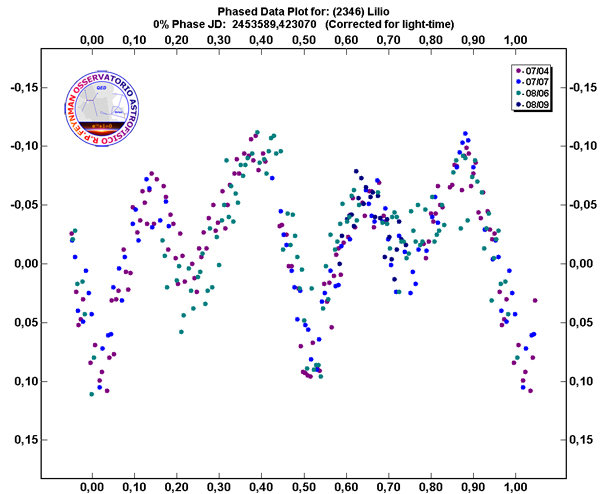
Curva di luce di (2346) Lilio. La presenza di ben quattro massimi e minimi fa pensare che forse potrebbe trattarsi di un asteroide binario, ma non è da escludersi la possibilità che si tratti solo di un oggetto dalla complicata morfologia.
Irregolarità macroscopiche nella forma sono evidenti anche nel caso di (126) Velleda. Sarà sicuramente interessante tornare a studiare questi oggetti durante le prossime apparizioni, quando le differenti condizioni geometriche di illuminazione potranno evidenziare o anche nascondere alcune delle caratteristiche presenti nelle curve di luce e quindi fornire ulteriori indicazioni sulla loro morfologia.
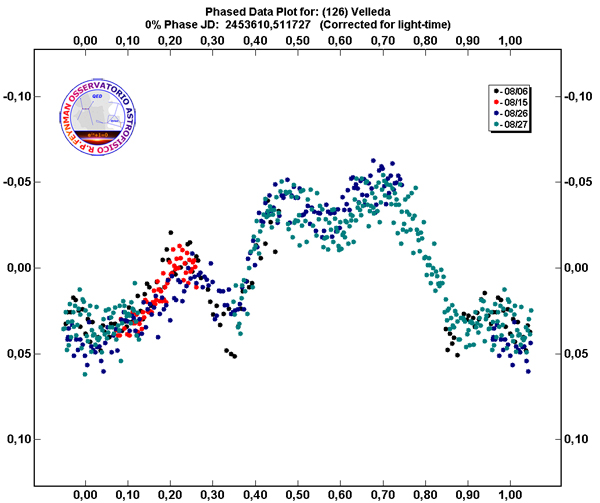
Curva di Luce di (126) Velleda, un asteroide caratterizzato da una morfologia piuttosto accidentata, dovuta probabilmente ad una tumultuosa esistenza, con frequenti collisioni con altri suoi simili.
Ha un certo fascino iniziare a misurare un asteroide di cui non se ne sa assolutamente niente. E’ come intraprendere l’esplorazione di un’isola che fino a quel momento era solo un punto su una mappa. E non è detto che non celi un piccolo tesoro.
Domenico Licchelli – 2015
Approfondimento
Mentre la determinazione del periodo di rotazione è normalmente cosa rapida e facile (una volta bastava un buon fotometro fotoelettrico, oggi un buon CCD), più complicata è la determinazione della forma e dell’asse di rotazione. In questo articolo voglio raccontarvi uno dei vari metodi, quello che ho usato più spesso (in quanto messo a punto proprio da … me) e che risulta anche il più semplice da spiegare geometricamente e senza utilizzare formule più o meno complicate.
L’ipotesi fondamentale che bisogna fare per poter arrivare a un risultato accettabile è che la forma dell’asteroide sia assimilabile a un ellissoide a tre assi (a>b>c), rotante attorno al semiasse minore c. Attenzione! Questo non vuol dire che tutti gli asteroidi siano forme di equilibrio, ma solo che, come tutti i frammenti collisionali, hanno forme più o meno allungate e non simmetriche. La rotazione intorno all’asse minore è comprovata dalla teoria e dalla casistica, e si lega a condizioni che si riferiscono al momento angolare.
Le forme a tre assi sono più che giustificabili, guardando i sassi di una spiaggia ciottolosa in cui il mare abbia smussato gli angoli delle pietre (Fig. 2).

Ammettiamo, quindi, che il nostro asteroide si presenti come un ellissoide a tre assi, rotante attorno all’asse minore. Magnifico. Tuttavia, noi continuiamo a vedere, da terra, solo un punto luminoso e quindi l’ellissoide può essere orientato in qualsiasi modo nella sua posizione celeste.
La sua prima curva di luce, in genere, ci aiuta già a capire la forma grossolana: se l’ampiezza, ossia la differenza tra massimi e minimi, è abbastanza rilevante vuol dire che l’ellissoide è piuttosto allungato. Come mai? Presto detto. Prendiamo ad esempio un oggetto che abbia l’asse di rotazione perfettamente perpendicolare alla linea di vista. In Fig. 3, nella parte alta, vi è l’ellissoide visto dal polo (e quindi l’ellisse mostra proprio gli assi maggiori a e b), mentre le due rappresentazioni sottostanti si riferiscono a vari istanti.
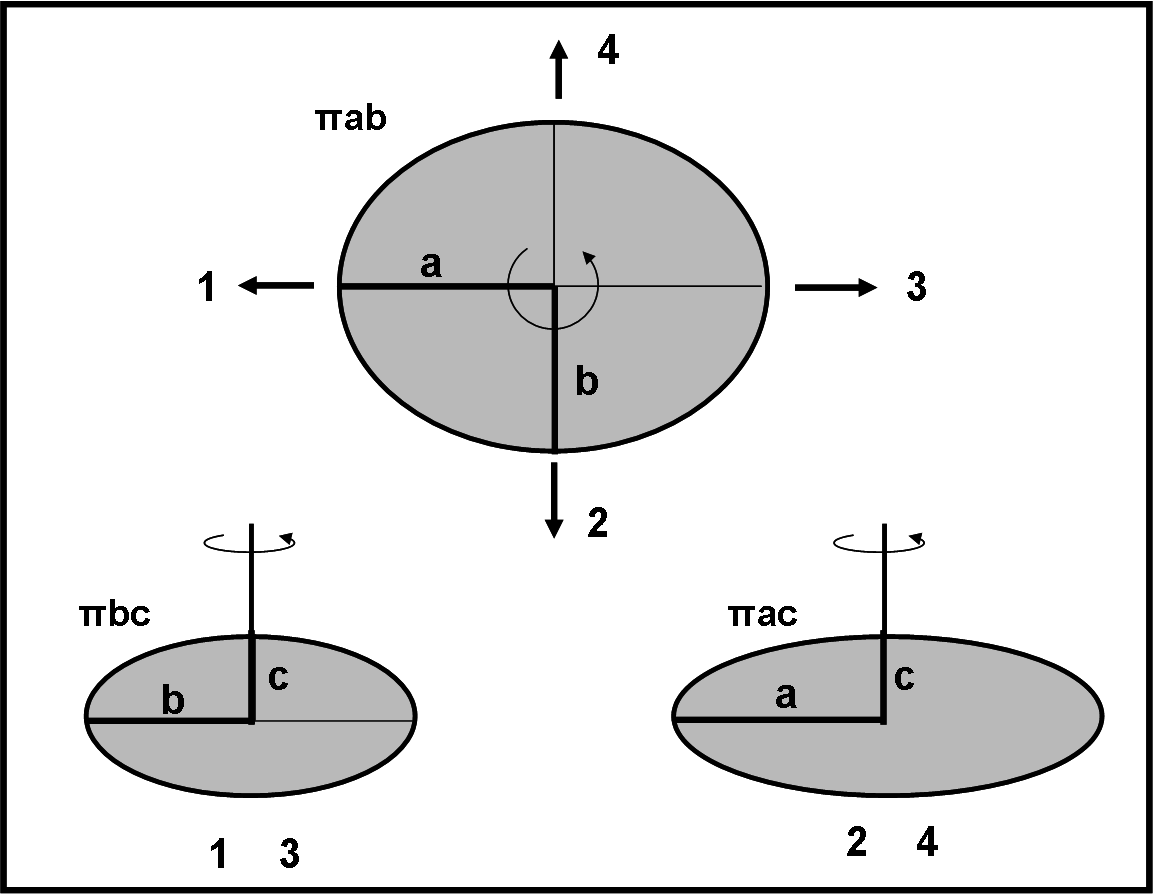
Figura 3. In alto un ellissoide a tre assi visto dalla direzione dell’asse polare. Durante la sua rotazione l’area rimane costante. Se, invece, viene visto dalle posizioni 1, 2, 3, 4 l’area cambia continuamente e passa da un minimo a un massimo. Come conseguenza, durante un intero periodo di rotazione d’identificano due massimi e due minimi di luce.
In particolare, l’area della superficie ellittica vista da terra passa da un minimo (1) quando si vede l’asse intermedio b (πbc) a un massimo (2) (dopo novanta gradi di rotazione) quando si vede l’asse maggiore a (πac). Poi, dopo altri 90°, di nuovo πbc (3), seguita da πac (4), per concludersi, infine, nuovamente con πbc (1). L’asse minore c si vede sempre, proprio perché l’asse di rotazione è perpendicolare alla linea di vista.
In questo caso così favorevole si potrebbe immediatamente risalire al rapporto tra gli assi maggiori dell’ellissoide (a/b), scrivendo la formula:
m2 – m1 = – 2.5 log (Imax/Imin) = – 2.5 log (Amax/Amin) = – 2.5 log (πac/ πbc) = – 2.5 log (a/b)
notando che m2 – m1 è proprio l’ampiezza della curva di luce in quanto è la differenza di magnitudine tra massimo e minimo, mentre l’intensità luminosa che entra nel logaritmo è, nel caso di luce riflessa, proporzionale solo all’area apparente vista dall’osservatore. In altre parole, più uno “specchio” è grande e più luce riflette.
Se fossimo sicuri di essere nelle condizioni della Fig. 3 avremmo già ottenuto un risultato importante. Purtroppo, esso è solo un caso fortunato, che, però, si verifica sempre (prima o poi) per qualsiasi asteroide e per qualsiasi orientazione del suo asse di rotazione. Basta avere pazienza. Ora vi mostro perché…
Consideriamo due casi estremamente particolari, ma molto indicativi. L’asteroide si trova su un’orbita circolare e complanare con quella terrestre. La direzione del suo asse di rotazione è perpendicolare all’orbita stessa (Fig. 4).
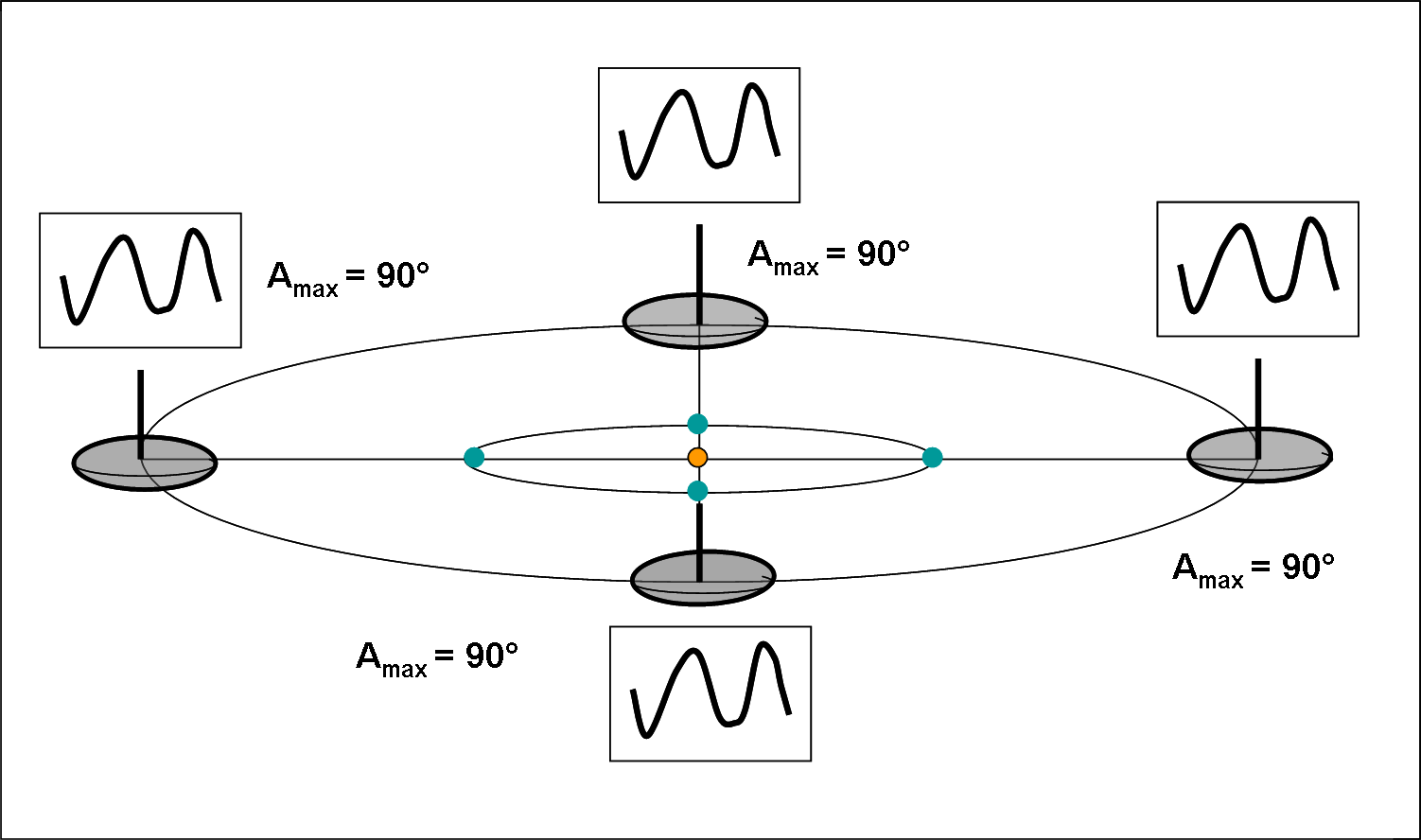
Figura 4. Asteroide e Terra rivolvono su orbite complanari e l’asse di rotazione è perpendicolare al piano orbitale.
Le mutue posizioni Terra-asteroide sono mostrate per 4 particolari opposizioni. In realtà, sarebbe stato inutile, in quanto l’angolo tra asse di rotazione e linea di vista rimane sempre uguale a 90° (visione equatoriale). In qualsiasi opposizione si osservi, si ricade nel caso di Fig. 3 (in basso). Otteniamo sempre la stessa ampiezza di curva di luce.
Già dalla prima curva di luce, si ricava subito il rapporto tra gli assi maggiori a/b, ma nessuna informazione sul rapporto a/c o b/c. Sappiamo anche la direzione dell’asse di rotazione (non variando l’ampiezza nelle varie opposizioni l’asse deve essere perpendicolare). Se facciamo un diagramma dove in ascissa mettiamo, ad esempio, la longitudine dell’asteroide e in ordinata l’ampiezza della curva di luce, otteniamo dei punti perfettamente allineati lungo una parallela all’asse delle ascisse.
Altrettanto peculiare, ma più interessante, il caso mostrato nella Fig. 5.
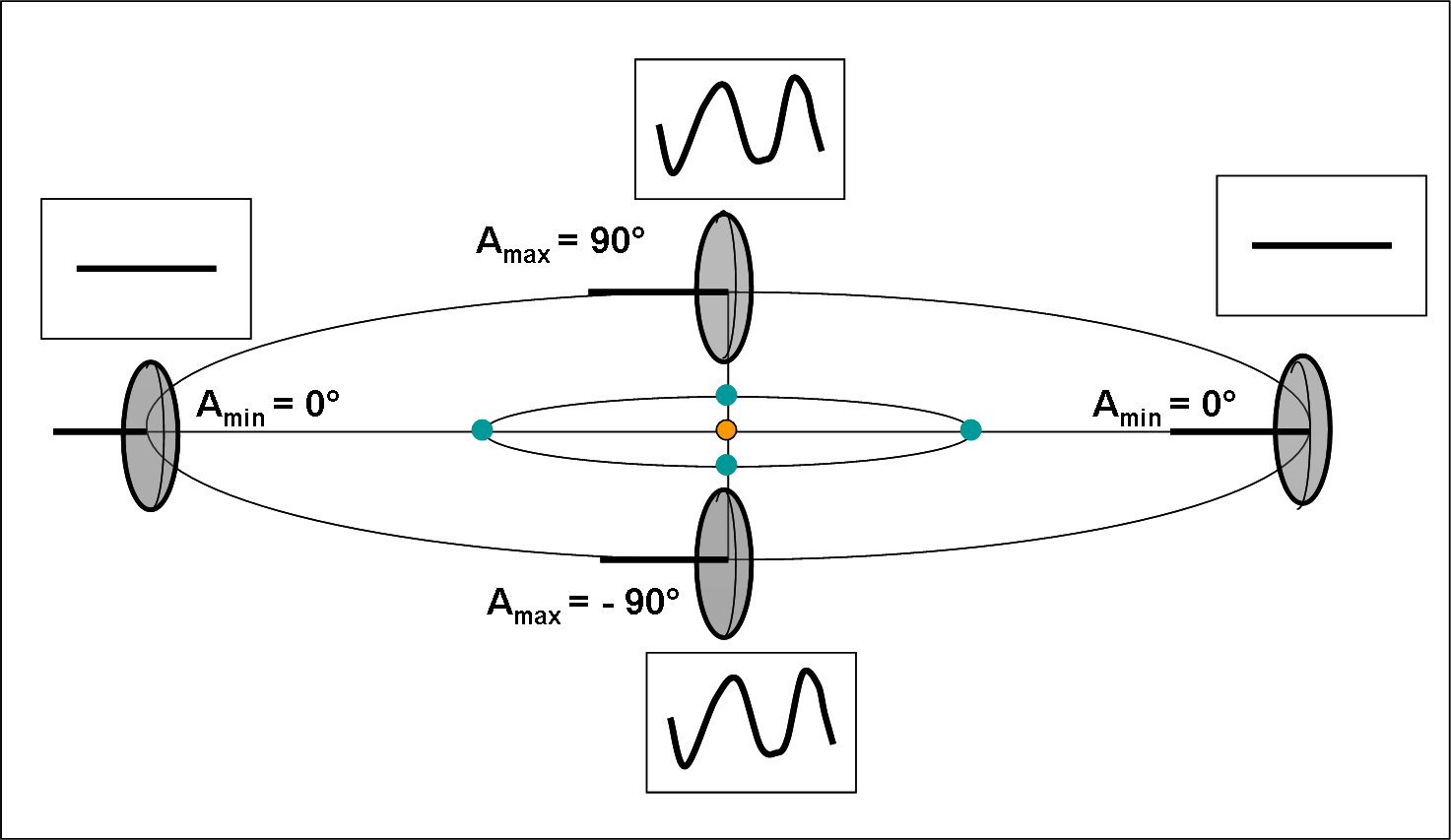
Figura 5. Come la Figura 4, ma l’asse di rotazione giace sul piano orbitale.
In questo caso le orbite sono sempre complanari, ma l’asse di rotazione giace sul piano orbitale (un po’ come Urano). Vi è allora un punto in cui la Terra vede l’asteroide proprio lungo l’asse di rotazione (posizione a destra), ossia l’osservatore non rileva nessuna variazione luminosa durante il periodo di rotazione dell’oggetto celeste (visione polare). Siamo, infatti, nel caso mostrato in alto nella Fig. 3. Per un opposizione che cada a 90° da questa si ha, invece, un angolo tra asse di rotazione e linea di vista uguale a 90° (come in Fig. 3, in basso) e quindi l’ampiezza della curva raggiunge il suo valore massimo (visione equatoriale). Dopo altri 90° ricadiamo nella visione polare (anche se si vede il polo opposto) e poi ancora nella visione equatoriale.
Nelle configurazioni intermedie tra questi quattro casi peculiari, l’asse di rotazione dell’asteroide forma un angolo variabile tra 0° e 90°, che prende il nome di angolo di aspetto A. In realtà l’angolo andrebbe da 0° a 180° o da – 90° a + 90°, a seconda di come si misuri. Questo fatto ha poca importanza (per adesso, ma ne parleremo più avanti), dato che abbiamo assunto come forma dell’asteroide quella di un ellissoide perfetto, la cui luminosità dipende solo dall’area apparente mostrata all’osservatore.
Al variare dell’angolo di aspetto, l’ampiezza assume valori intermedi tra il valore minimo, uguale a zero (visione polare), e il valore massimo (visione equatoriale). Osservazioni eseguite in varie opposizioni permettono di costruire la curva ampiezza-longitudine. Questa volta non è più una retta parallela all’asse delle ascisse, ma una curva continua che assomiglia, in qualche modo, a una curva di luce. Il valore massimo è sicuramente la visione equatoriale e quindi ci permette di conoscere nuovamente a/b. Inoltre, la posizione in cui l’ampiezza diventa zero, indica proprio la longitudine del polo.
In questo caso peculiare, sappiamo anche che la latitudine della direzione dell’asse di rotazione è zero, dato che l’ampiezza minima è nulla e quindi l’asse deve giacere sul piano orbitale dell’asteroide. Calcolando, infine, la differenza di magnitudine tra la visione polare (valore costante durante l’intera rotazione) e quella della visione equatoriale al massimo della curva di luce, si ottiene subito anche il rapporto tra b e c. Si usa la solita formula:
mP – mE = – 2.5 log (A(polare)/Amax(equatoriale)) = – 2.5 log (πab/ πac) = – 2.5 log (b/c)
Il “caso” è risolto completamente.
Come già detto, però, questa è una situazione del tutto peculiare, molto didattica, ma poco realistica. La situazione “normale” è decisamente più complicata. Ciò che capita è quanto raffigurato in Fig. 6.
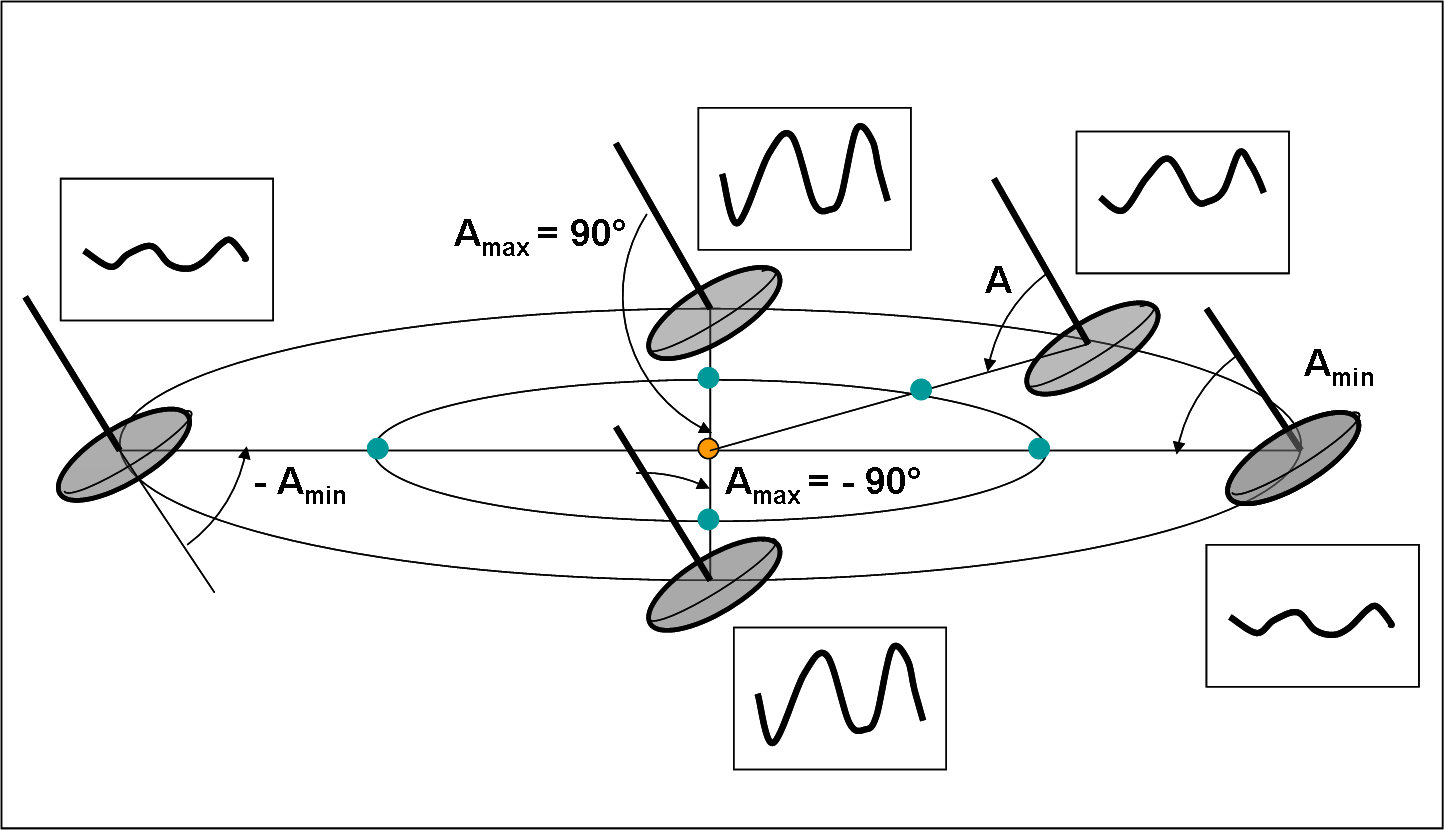
Figura 6. Come Figura 5, ma questa volta l’asse forma un angolo qualsiasi col piano orbitale.
L’inclinazione del’asse di rotazione sul piano orbitale è diversa da 0° e da 90° (o, se preferite, la latitudine, nel caso di orbita complanare con quella dell’eclittica). Tuttavia, dobbiamo notare due cose importanti. Anche in questo caso realistico, prima o poi, si avrà un’opposizione con una visione equatoriale (angolo di aspetto A uguale a 90°).
Se questa asserzione vi lascia un po’ dubbiosi, pensate alle stagioni terrestri. Esistono sempre due punti in cui l’asse di rotazione della Terra è perpendicolare al piano dell’eclittica e questi sono gli equinozi. Essi vi sono comunque, indipendentemente da quanto vale l’angolo tra asse ed eclittica. La visione polare è invece impossibile da ottenere e si ha soltanto un valore minimo di ampiezza, in corrispondenza, però, della posizione a 90° dalla visione equatoriale. In altre parole, il minimo della curva ampiezza-longitudine indica, ancora una volta, la longitudine del polo dell’asteroide. Nel caso terrestre questi sono i punti dei solstizi. Alcuni esempi di curve ampiezza-longitudine sono riportate nella Fig. 7.
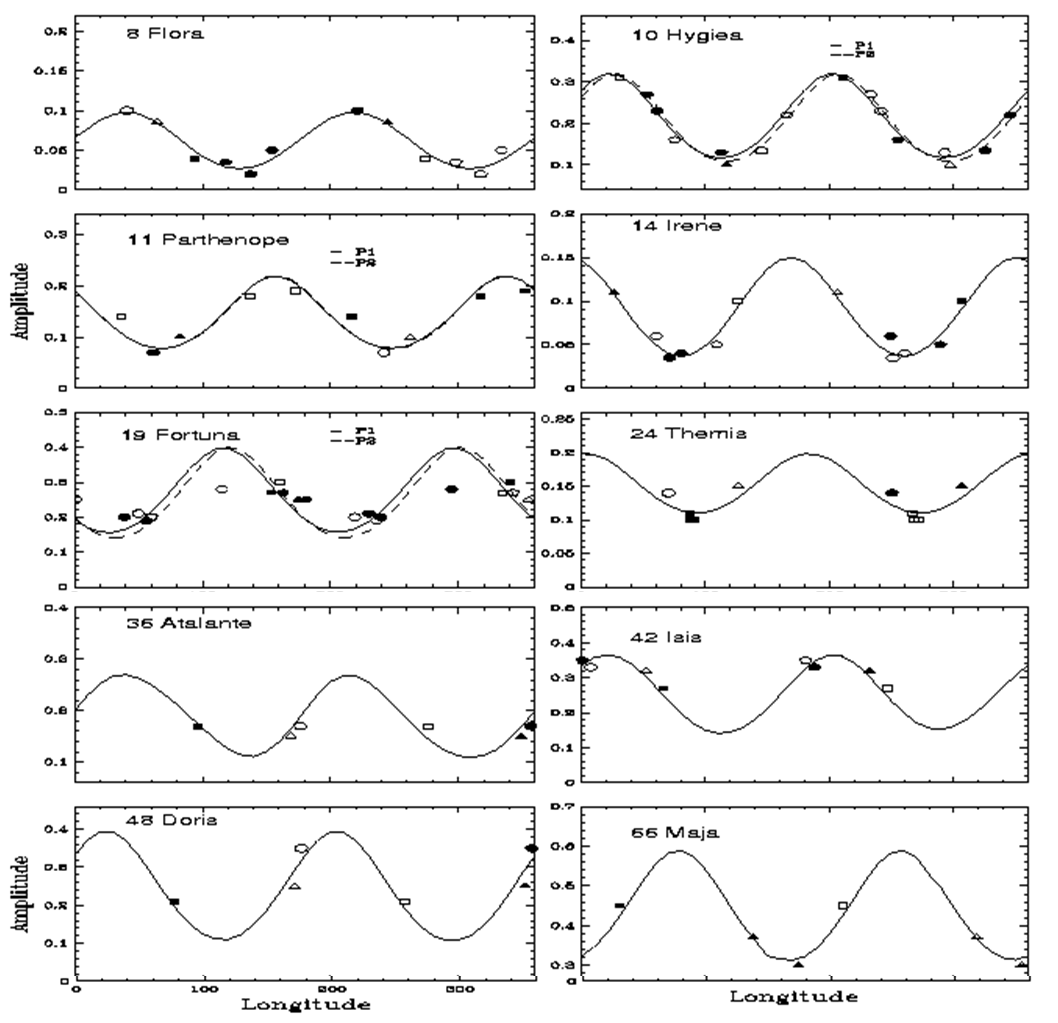
Figura 7. Alcune curve ampiezza-longitudine. Qualsiasi asteroide raggiunge sempre il massimo di ampiezza (visione equatoriale). Il minimo, invece, può essere più alto o più basso, Indica comunque abbastanza bene la longitudine del polo.
Possiamo calcolare, come al solito, il rapporto a/b, sfruttando l’ampiezza misurata nella visione equatoriale (che si ha sempre, ripeto). Resta più problematica la determinazione del rapporto b/c e della latitudine del polo. Ci aiuta la Fig. 8 che riporta la situazione per un’opposizione e per un orientamento qualsiasi dell’asse di rotazione. L’osservatore vede, in realtà, una proiezione dell’asteroide-ellissoide su un piano perpendicolare alla linea di vista. Essa si ottiene, visivamente, come la sezione perpendicolare di un cilindro ellittico che abbia la direzione Terra-asteroide come asse e che sia tangente all’asteroide.
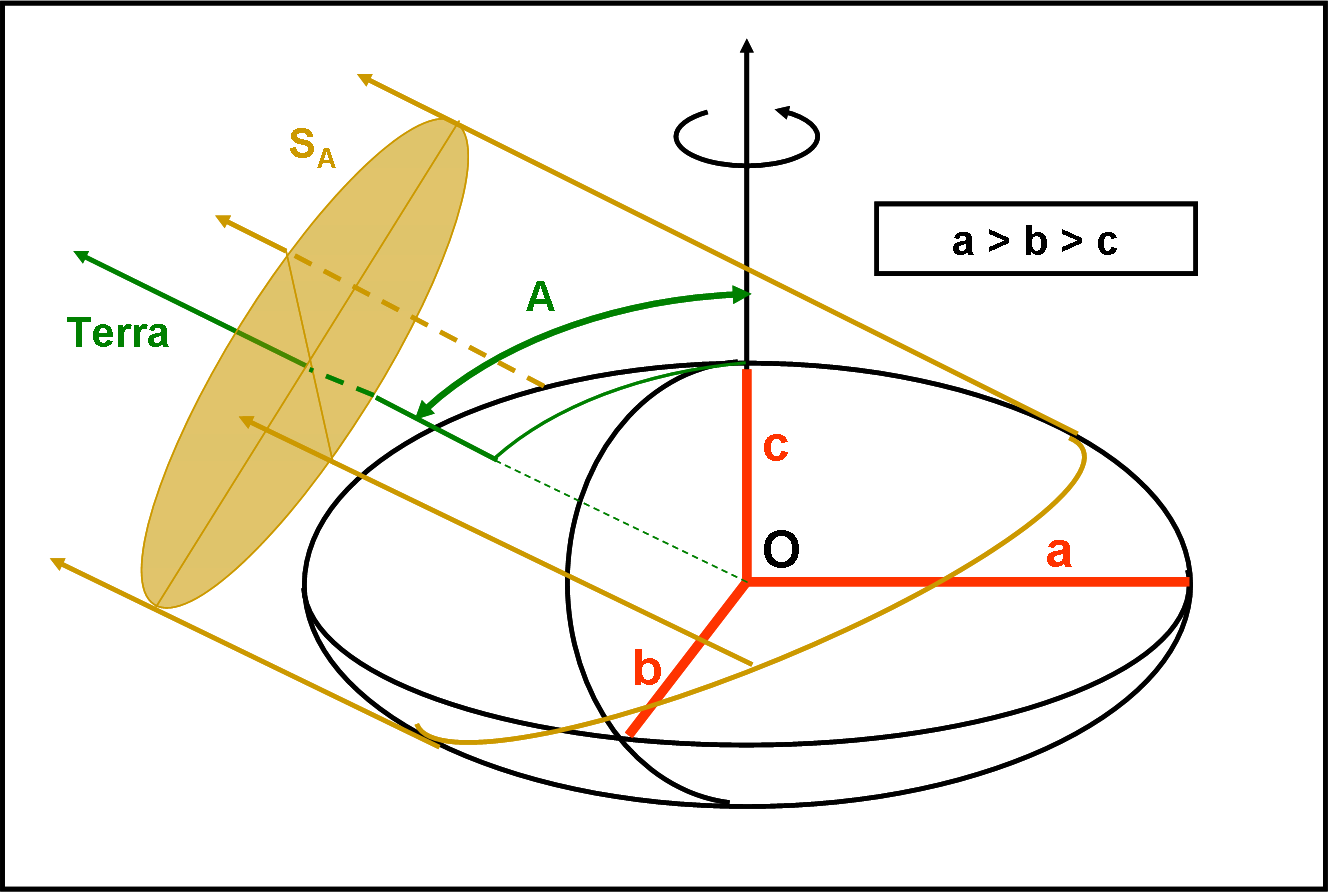
Figura 8
L’angolo tra asse del cilindro e asse di rotazione è proprio l’angolo di aspetto A. La proiezione è anch’essa un’ellisse, ovviamente, ma i suoi assi sono, momento per momento, delle funzioni abbastanza semplici che legano angolo di aspetto e rapporti tra i semi-asse dell’asteroide.
Particolare rilevanza hanno, ovviamente, quelli relativi al massimo e al minimo della curva di luce. Non intendo sviluppare le formule, in quanto approfittano di un po’ di trigonometria e di qualche passaggio più o meno noioso, ma posso assicurarvi che esiste una soluzione che dona sia la forma che i rapporti tra gli assi.
Abbiamo fatto qualche ipotesi restrittiva, ma le applicazioni ai casi reali confermano che l’approccio è più che sufficiente per una determinazione abbastanza accurata. I risultati ottenuti per Eros, Kleopatra e Vesta (anche se in modo più elaborato) sono perfettamente in accordo con quanto osservato “in loco” (Eros e Vesta) o attraverso le immagini radar (Kleopatra).
La determinazione dell’asse di rotazione resta, comunque, un po’ ambigua. In altre parole, esistono quasi sempre due soluzioni altrettanto valide. Questo fatto si può notare nella Fig. 9.

Figura 9. Si vedrebbe la stessa superficie apparente per qualsiasi posizione dell’asse lungo il cono con centro nella posizione dell’asteroide e ampiezza uguale all’angolo di aspetto.
Qualsiasi sia la configurazione dell’asteroide nello spazio, la curva di luce non cambia se l’asse di rotazione descrive un cono circolare, di ampiezza uguale all’angolo di aspetto A.
Fortunatamente, questa enorme ambiguità si ha solo per una singola opposizione. Se ne abbiamo altre e raffiguriamo, nel piano longitudine-latitudine celeste, le circonferenze che hanno centro nella posizione dell’asteroide e raggio uguale all’angolo di aspetto, esse hanno due soli punti in comune (Fig. 10).
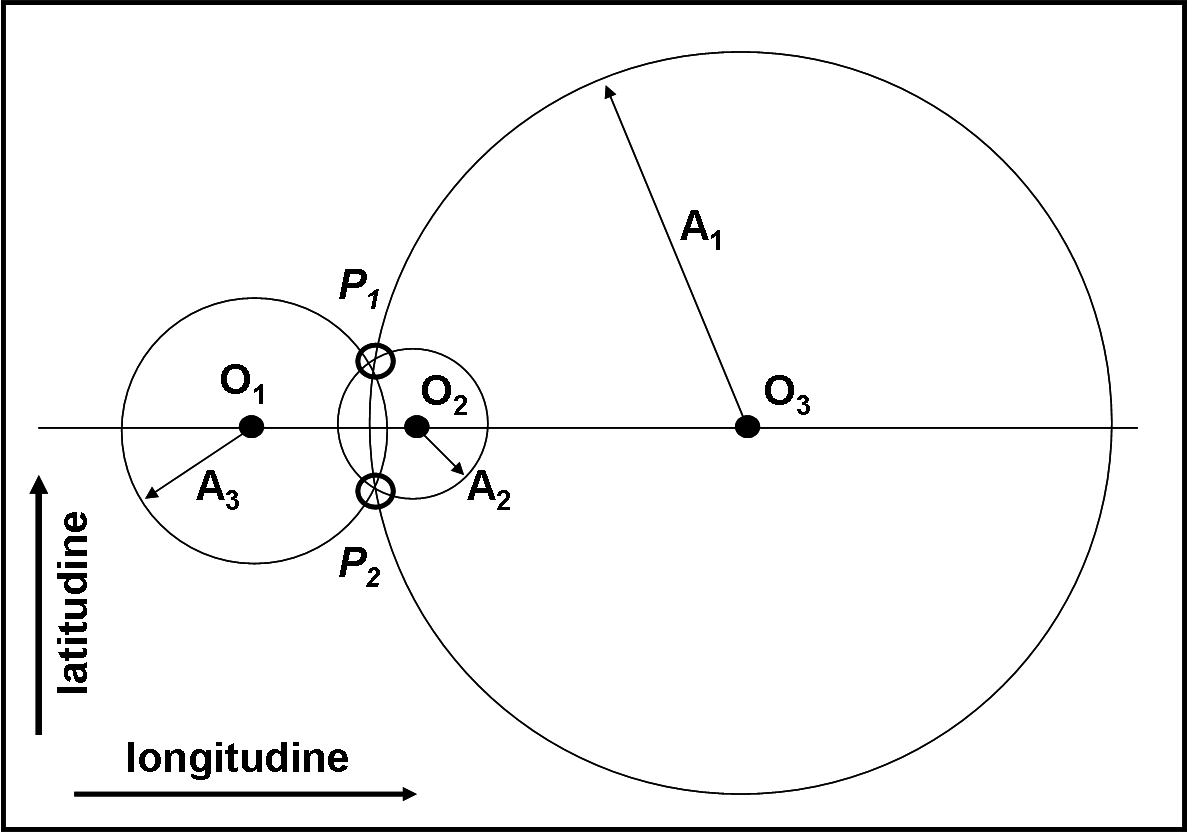
Figura 10. Se l’orbita non è inclinata ed è circolare, l’ambiguità tra i due poli non non può essere risolta.
La loro longitudine e latitudine sono i possibili valori del polo dell’asteroide. In modo analitico questo fatto si traduce dicendo che l’angolo di aspetto è calcolato solo in valore assoluto (ossia può essere sia positivo che negativo, come già accennato in precedenza).
Per risolvere l’ambiguità, è necessario che l’orbita non sia complanare con l’eclittica e, magari, che sia anche piuttosto ellittica. In questi casi vi è una piccola differenza tra le due soluzioni: una delle due intersezioni è meno “buona” dell’altra.
Tuttavia, dato che gli errori sono molti (macchie di albedo, forma non assimilabile completamente a un ellissoide a tre assi, rugosità superficiale, effetto dell’angolo di fase solare sulla luminosità della superficie esposta all’osservatore (ossia l’ombra su una superficie convessa), ecc.), l’ambiguità è difficilmente risolta e le differenze riscontrate negli errori stimati per le due soluzioni sono comparabili o minori di quelli introdotti da altre cause.
In ogni modo, si ottengono valori più che accettabili per lavori di tipo statistico e anche per pianificare missioni spaziali dirette agli asteroidi, per le quali è necessario avere una stima dell’asse di rotazione e della forma.

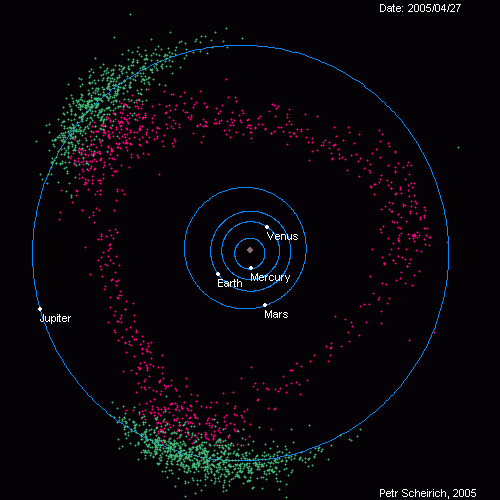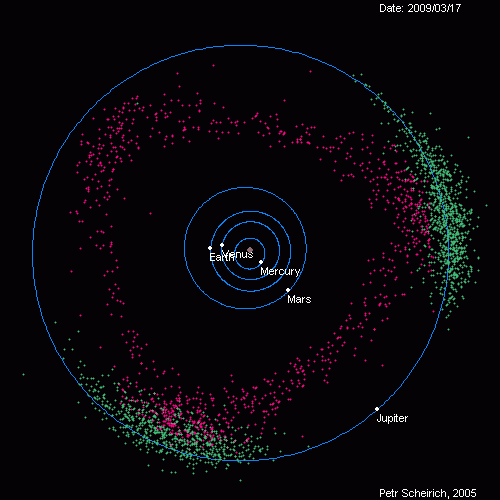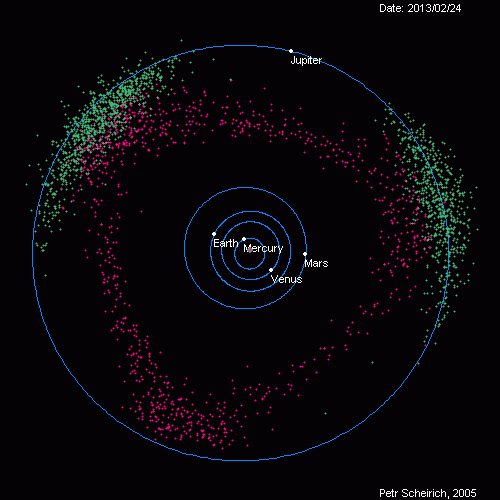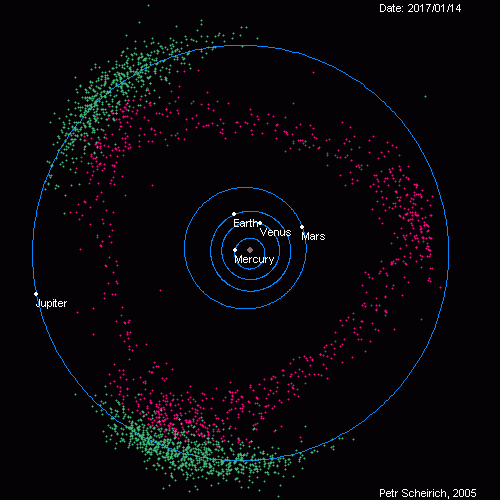 Queste lacune coincidono con orbite fortemente caotiche situate in corrispondenza di valori del semiasse maggiore orbitale che portano ad una ripetizione delle posizioni relative di Sole, Giove e dell’asteroide. Ad esempio, una lacuna di Kirkwood è situata in corrispondenza di orbite caratterizzate da un periodo di rivoluzione pari ad 1/3 di quello gioviano. Questa lacuna si trova ad una distanza di 2.5 UA e in essa un eventuale asteroide, ogni tre rivoluzioni, si troverebbe nella stessa posizione di Giove. Questo dà luogo ad una risonanza di moto medio che produce un aumento della forza di Giove. Il povero asteroide che si trova a passare da questa regione viene espulso e immesso in un orbita differente tipicamente caratterizzata da un periodo minore e quindi più vicina a noi. Esistono poi due gruppi di asteroidi che si muovono in sincronia con Giove, lungo la sua stessa orbita. Questi asteroidi sono chiamati Troiani, una parte di essi precede Giove mentre l’altra lo segue.
Queste lacune coincidono con orbite fortemente caotiche situate in corrispondenza di valori del semiasse maggiore orbitale che portano ad una ripetizione delle posizioni relative di Sole, Giove e dell’asteroide. Ad esempio, una lacuna di Kirkwood è situata in corrispondenza di orbite caratterizzate da un periodo di rivoluzione pari ad 1/3 di quello gioviano. Questa lacuna si trova ad una distanza di 2.5 UA e in essa un eventuale asteroide, ogni tre rivoluzioni, si troverebbe nella stessa posizione di Giove. Questo dà luogo ad una risonanza di moto medio che produce un aumento della forza di Giove. Il povero asteroide che si trova a passare da questa regione viene espulso e immesso in un orbita differente tipicamente caratterizzata da un periodo minore e quindi più vicina a noi. Esistono poi due gruppi di asteroidi che si muovono in sincronia con Giove, lungo la sua stessa orbita. Questi asteroidi sono chiamati Troiani, una parte di essi precede Giove mentre l’altra lo segue.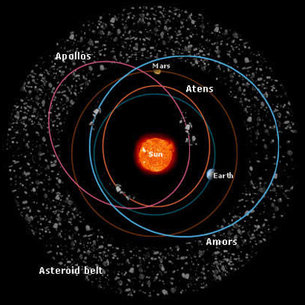 Come possiamo notare in figura, gli Atens nel loro cammino attorno al Sole, incrociano l’orbita terrestre. Hanno un semiasse maggiore orbitale inferiore a 1 UA, quindi per la maggior parte del tempo si trovano all’interno dell’orbita terrestre. Gli asteroidi della popolazione Apollo, al contrario, trascorrono più tempo al di fuori dell’orbita terrestre ma quando si avvicinano al perielio incrociano anch’essi l’orbita terrestre per passare al suo interno. Gli Amor, invece, non intercettano mai l’orbita terrestre durante il loro cammino. Essi, infatti, al perielio vengono a trovarsi ad una distanza dal Sole compresa tra 1.017 e 1.3 UA, maggiore pertanto della distanza Terra-Sole, ma non per questo sono meno pericolosi. Tutti questi oggetti evolvono in maniera caotica quindi la loro differenziazione in gruppi può essere meno netta. In base ad analisi spettrali la popolazione asteroidale è stata suddivisa in differenti classi tassonomiche di cui ricordiamo le più numerose che sono le classi S, C, P, D ed M. Gli asteroidi appartenenti alla classe S rivelano la presenza di silicati e presentano un’albedo di gran lunga maggiore rispetto agli asteroidi di classe C. inoltre, hanno semiassi maggiori con valori compresi tra 2 e 2.5 UA dal Sole, mentre gli asteroidi della classe C raggiungono una distanza massima di 3.1 UA. All’interno della fascia principale predominano i corpi di classe S. Si tratta di un gruppo variegato che comprende sia corpi che hanno attraversato una fase di fusione, sia corpi che non sono mai stati allo stato fuso. Gli asteroidi più vicini a Marte sono composti prevalentemente da materiali rocciosi mescolati con ferro, mentre quelli situati esternamente e quindi più prossimi a Giove sembrano tutti corpi primitivi con composizione abbastanza simile a quella della nebulosa primordiale dalla quale ha avuto origine l’intero Sistema Solare. Questi oggetti appartengono alle classi C, P e D.
Come possiamo notare in figura, gli Atens nel loro cammino attorno al Sole, incrociano l’orbita terrestre. Hanno un semiasse maggiore orbitale inferiore a 1 UA, quindi per la maggior parte del tempo si trovano all’interno dell’orbita terrestre. Gli asteroidi della popolazione Apollo, al contrario, trascorrono più tempo al di fuori dell’orbita terrestre ma quando si avvicinano al perielio incrociano anch’essi l’orbita terrestre per passare al suo interno. Gli Amor, invece, non intercettano mai l’orbita terrestre durante il loro cammino. Essi, infatti, al perielio vengono a trovarsi ad una distanza dal Sole compresa tra 1.017 e 1.3 UA, maggiore pertanto della distanza Terra-Sole, ma non per questo sono meno pericolosi. Tutti questi oggetti evolvono in maniera caotica quindi la loro differenziazione in gruppi può essere meno netta. In base ad analisi spettrali la popolazione asteroidale è stata suddivisa in differenti classi tassonomiche di cui ricordiamo le più numerose che sono le classi S, C, P, D ed M. Gli asteroidi appartenenti alla classe S rivelano la presenza di silicati e presentano un’albedo di gran lunga maggiore rispetto agli asteroidi di classe C. inoltre, hanno semiassi maggiori con valori compresi tra 2 e 2.5 UA dal Sole, mentre gli asteroidi della classe C raggiungono una distanza massima di 3.1 UA. All’interno della fascia principale predominano i corpi di classe S. Si tratta di un gruppo variegato che comprende sia corpi che hanno attraversato una fase di fusione, sia corpi che non sono mai stati allo stato fuso. Gli asteroidi più vicini a Marte sono composti prevalentemente da materiali rocciosi mescolati con ferro, mentre quelli situati esternamente e quindi più prossimi a Giove sembrano tutti corpi primitivi con composizione abbastanza simile a quella della nebulosa primordiale dalla quale ha avuto origine l’intero Sistema Solare. Questi oggetti appartengono alle classi C, P e D.